Boolean model (probability theory)
The Boolean model for a random subset of the plane (or higher dimensions, analogously) is one of the simplest and most tractable models in stochastic geometry. Take a Poisson point process of rate  in the plane and make each point be the center of a random set; the resulting union of overlapping sets is a realization of the Boolean model
in the plane and make each point be the center of a random set; the resulting union of overlapping sets is a realization of the Boolean model  . More precisely, the parameters are
. More precisely, the parameters are  and a probability distribution on compact sets; for each point
and a probability distribution on compact sets; for each point 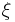 of the Poisson point process we pick a set
of the Poisson point process we pick a set  from the distribution, and then define
from the distribution, and then define  as the union
as the union 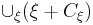 of translated sets.
of translated sets.
To illustrate tractability with one simple formula, the mean density of  equals
equals 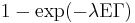 where
where  denotes the area of
denotes the area of  . The classical theory of stochastic geometry develops many further formulas – see [1] [2].
. The classical theory of stochastic geometry develops many further formulas – see [1] [2].
As related topics, the case of constant-sized discs is the basic model of continuum percolation [3] and the low-density Boolean models serve as a first-order approximations in the study of extremes in many models [4].
References
- ^ Stoyan, D., Kendall, W.S. and Mecke, J. (1987). Stochastic geometry and its applications. Wiley.
- ^ Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer.
- ^ Meester, R. and Roy, R. (2008). Continuum Percolation. Cambridge University Press.
- ^ Aldous, D. (1988). Probability Approximations via the Poisson Clumping Heuristic. Springer.